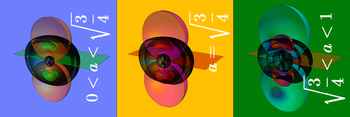Black hole surface pop

• Author(s) / Creator(s)

  • Boos, Jens

• Black holes belong to the most fascinating objects in our Universe, and they challenge the way we think about space and time. My research involves studying both mathematical and physical properties of black holes, and how they can help us to learn something new about the Universe we live in. With this contribution, I'm trying to bridge the gap between theoretical physics and modern art by mixing scientific results and the concept of pop art.
  My image contains three computer-generated plots of a rotating black hole, where the rotation speed "a" increases from left to right. The black surfaces correspond to the various horizons (the "membranes," that once you pass them, you can never get out again). The other surfaces have a more involved meaning, in that they visualize the vanishing of so-called curvature invariants.
  Look at the green lobes in the leftmost picture, and track their shape as the rotation speed "a" increases to the right. In the middle one, for a critical value, they touch the horizon at the north and south pole, and in the right picture they protrude outside of the horizon. Mathematically it means that only for the first two pictures we can think of the black hole horizon as a surface in flat three-dimensional space, and not for the third one.
  Based on J.B. and A. Favaro, "Kerr principal null directions from Bel--Robinson and Kummer surfaces," http://www.arxiv.org/abs/1703.10791 . // Project of Study: PhD // Faculty/Department: Faculty of Science, Department of Physics // Place of Creation: Computer-generated images // Award: Semi-finalist Prize, Images of Research Competition 2018

• Date created

  2018-01-01

• Subjects / Keywords

  • Research image

• Type of Item

  Image

• DOI

  https://doi.org/10.7939/R3GB1XX85

• License

  Attribution 4.0 International